Teorema de bayes

TEOREMA DE BAYES

El teorema de Bayes es un método muy útil para calcular probabilidades de una partición, una vez se conoce que un suceso concreto ya ha ocurrido. Por tanto, si B es el suceso que ha ocurrido y A es una partición del espacio muestral, la fórmula de este teorema es: P(A|B)=P(A)·P(B|A)/P(B).

formula

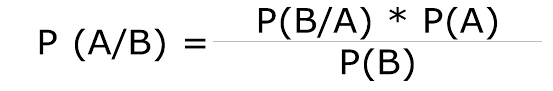
A, B= eventos

P(A/B)= la probabilidad de A dado B P(B/A)= la probabilidad de B dado A

P(A), P(B)= las probabilidades independientes de A y B

probabilidad

a posteriori

• La probabilidad a posteriori se calcula con el teorema de Bayes. Es la probabilidad de que el suceso que hemos obtenido esté dentro de un grupo (partición) concreto. La fórmula para calcular esta probabilidad es:
  

P(A|B)=P(A)·P(B|A)/P(B).

probabilidad

a priori

• Se llaman probabilidades iniciales o probabilidades a priori a las probabilidades P(Aj) de los sucesos que forman las particiones del espacio muestral.

Por ejemplo, si nos dicen que en una bolsa hay bolas rojas, verdes y azules, y cada una de estas se subdividen en color liso o rayado, las probabilidades a priori serían la de sacar una pelota roja, una verde o una azul, independientemente de si es lisa o rayada

En una escuela, la probabilidad de que a un alumno seleccionado al azar le guste el helado es del 60 %, mientras que la probabilidad de que a un alumno le guste el pastel es del 36 %. Además, se sabe que la probabilidad de que a un alumno le guste el pastel dado que le gusta el helado es del 40 %. Calcular la probabilidad de que a un alumno le guste el helado, dado que le gusta el pastel.

Solución:

Primero definimos los 2 eventos con los que vamos a trabajar:

• h: que a un alumno le guste el helado.
  
• t: que a un alumno le guste la torta.
  

Tenemos los siguientes datos:

• P(h) = 0,6.
  
• P(t) = 0,36.
  
• P(t|h) = 0,4.
  

Nos piden calcular P(h|t).

Aplicamos el teorema de Bayes:

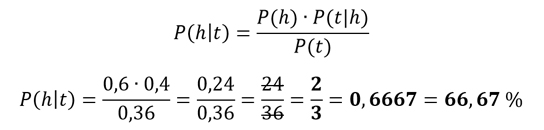
EJEMPLO

Entonces, la probabilidad de que un alumno le guste el helado dado que le gusta el pastel es de 0,6667 o 66,67 %.